【游戏算法】 - 四叉树

宋 游戏开发
  2020-11-27 22:16:55 2020-11-27 22:16:55 创建   2021-03-15 20:30:55 2021-03-15 20:30:55 更新      2.3k 字  13 分钟

四叉树

四叉树通过递归地将二维空间划分为四个象限（左上、左下、右上、右下），形成一个层次化的树形结构。每个节点代表一个矩形区域，如果该区域内的元素数量超过设定阈值，节点会进一步分裂为四个子节点。这种分层结构使得四叉树在处理大规模空间数据时能够显著降低查询和更新的复杂度。
四叉树-1
游戏开发中的四叉树最常见的应用是碰撞检测的优化，使用四叉树可快速过滤不在同一区域的对象，减少不必要的碰撞计算。
四叉树-2
过滤机制
层级递归查询：当需要检测某个对象是否与其他对象发生碰撞时，四叉树会从根节点开始，递归地向下查询可能包含碰撞对象的子节点。例如：
如果目标对象位于某个子区域，则只需检查该子区域内的对象。
如果目标对象跨越多个子区域（如边界附近），则将其保留在父节点中，并检查所有相关子区域。
排除无关区域：如果两个对象所在的区域完全不重叠（例如一个在左上象限，另一个在右下象限），则可以直接跳过碰撞检测，避免不必要的计算。

代码实现

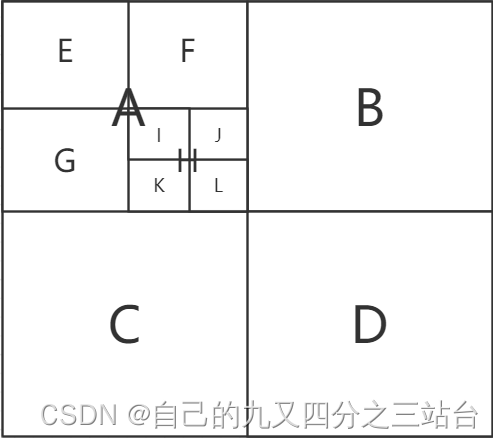
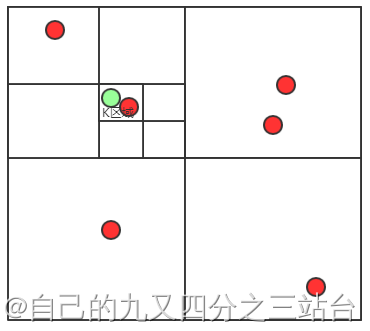
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <vector>
#include <memory>
#include <cmath>

struct Point {
    float x, y;
};

class Quadtree {
private:
    struct Node {
        float x, y, width;
        std::vector<Point> points;
        std::unique_ptr<Node> ne, nw, se, sw;
        
        Node(float x, float y, float width) 
            : x(x), y(y), width(width), ne(nullptr), nw(nullptr), se(nullptr), sw(nullptr) {}
        
        ~Node() {
            ne.reset();
            nw.reset();
            se.reset();
            sw.reset();
        }
        
        bool insert(Node*& node, const Point& p, int depth) {
            if (!contains(node, p)) return false;
            
            if (node->points.size() < 4 && !node->ne) {
                node->points.push_back(p);
                return true;
            }
            
            if (!node->ne) {
                split(node);
            }
            
            if (insert(node->ne.get(), p, depth+1)) return true;
            if (insert(node->nw.get(), p, depth+1)) return true;
            if (insert(node->se.get(), p, depth+1)) return true;
            if (insert(node->sw.get(), p, depth+1)) return true;
            
            return false;
        }
        
        bool contains(Node* node, const Point& p) {
            return p.x >= node->x - node->width/2 && 
                   p.x <= node->x + node->width/2 &&
                   p.y >= node->y - node->width/2 &&
                   p.y <= node->y + node->width/2;
        }
        
        void split(Node* node) {
            float half = node->width / 2;
            
            node->ne = std::make_unique<Node>(node->x + half/2, node->y + half/2, half);
            node->nw = std::make_unique<Node>(node->x - half/2, node->y + half/2, half);
            node->se = std::make_unique<Node>(node->x + half/2, node->y - half/2, half);
            node->sw = std::make_unique<Node>(node->x - half/2, node->y - half/2, half);
            
            for (auto& p : node->points) {
                insert(node->ne.get(), p, 0);
                insert(node->nw.get(), p, 0);
                insert(node->se.get(), p, 0);
                insert(node->sw.get(), p, 0);
            }
            
            node->points.clear();
        }
        
        std::vector<Point> query(Node* node, float minX, float maxX, float minY, float maxY) {
            std::vector<Point> result;
            
            if (!intersects(node, minX, maxX, minY, maxY)) return result;
            
            if (!node->ne) {
                for (auto& p : node->points) {
                    if (p.x >= minX && p.x <= maxX && p.y >= minY && p.y <= maxY) {
                        result.push_back(p);
                    }
                }
                return result;
            }
            
            auto neRes = query(node->ne.get(), minX, maxX, minY, maxY);
            auto nwRes = query(node->nw.get(), minX, maxX, minY, maxY);
            auto seRes = query(node->se.get(), minX, maxX, minY, maxY);
            auto swRes = query(node->sw.get(), minX, maxX, minY, maxY);
            
            result.insert(result.end(), neRes.begin(), neRes.end());
            result.insert(result.end(), nwRes.begin(), nwRes.end());
            result.insert(result.end(), seRes.begin(), seRes.end());
            result.insert(result.end(), swRes.begin(), swRes.end());
            
            return result;
        }
        
        bool intersects(Node* node, float minX, float maxX, float minY, float maxY) {
            return !(maxX < node->x - node->width/2 || 
                    minX > node->x + node->width/2 ||
                    maxY < node->y - node->width/2 ||
                    minY > node->y + node->width/2);
        }
    };
    
    std::unique_ptr<Node> root;
    int maxDepth;
    
public:
    Quadtree(float rootX, float rootY, float rootWidth, int maxDepth = 16)
        : root(std::make_unique<Node>(rootX, rootY, rootWidth)), maxDepth(maxDepth) {}
    
    void insert(const Point& p) {
        root->insert(root.get(), p, 0);
    }
    
    std::vector<Point> query(float minX, float maxX, float minY, float maxY) {
        return root->query(root.get(), minX, maxX, minY, maxY);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
using System;
using System.Collections.Generic;

public struct Point
{
    public float X { get; }
    public float Y { get; }
    
    public Point(float x, float y)
    {
        X = x;
        Y = y;
    }
}

public class Quadtree
{
    private class Node
    {
        public float X { get; }
        public float Y { get; }
        public float Width { get; }
        public List<Point> Points { get; } = new List<Point>();
        public Node Ne { get; private set; }
        public Node Nw { get; private set; }
        public Node Se { get; private set; }
        public Node Sw { get; private set; }
        private readonly int MaxCapacity = 4;
        
        public Node(float x, float y, float width)
        {
            X = x;
            Y = y;
            Width = width;
        }
        
        public bool Insert(Point p)
        {
            if (!Contains(p)) return false;
            
            if (Points.Count < MaxCapacity && (Ne == null))
            {
                Points.Add(p);
                return true;
            }
            
            if (Ne == null)
            {
                Split();
            }
            
            if (Ne.Insert(p)) return true;
            if (Nw.Insert(p)) return true;
            if (Se.Insert(p)) return true;
            if (Sw.Insert(p)) return true;
            
            return false;
        }
        
        private bool Contains(Point p)
        {
            return p.X >= X - Width/2 && 
                   p.X <= X + Width/2 &&
                   p.Y >= Y - Width/2 &&
                   p.Y <= Y + Width/2;
        }
        
        private void Split()
        {
            float half = Width / 2;
            
            Ne = new Node(X + half/2, Y + half/2, half);
            Nw = new Node(X - half/2, Y + half/2, half);
            Se = new Node(X + half/2, Y - half/2, half);
            Sw = new Node(X - half/2, Y - half/2, half);
            
            foreach (var p in Points)
            {
                Ne.Insert(p);
                Nw.Insert(p);
                Se.Insert(p);
                Sw.Insert(p);
            }
            
            Points.Clear();
        }
        
        public List<Point> Query(float minX, float maxX, float minY, float maxY)
        {
            var result = new List<Point>();
            
            if (!Intersects(minX, maxX, minY, maxY)) return result;
            
            if (Ne == null)
            {
                foreach (var p in Points)
                {
                    if (p.X >= minX && p.X <= maxX && p.Y >= minY && p.Y <= maxY)
                    {
                        result.Add(p);
                    }
                }
                return result;
            }
            
            result.AddRange(Ne.Query(minX, maxX, minY, maxY));
            result.AddRange(Nw.Query(minX, maxX, minY, maxY));
            result.AddRange(Se.Query(minX, maxX, minY, maxY));
            result.AddRange(Sw.Query(minX, maxX, minY, maxY));
            
            return result;
        }
        
        private bool Intersects(float minX, float maxX, float minY, float maxY)
        {
            return !(maxX < X - Width/2 || 
                    minX > X + Width/2 ||
                    maxY < Y - Width/2 ||
                    minY > Y + Width/2);
        }
    }
    
    private Node root;
    private readonly int maxDepth;
    
    public Quadtree(float rootX, float rootY, float rootWidth, int maxDepth = 16)
    {
        root = new Node(rootX, rootY, rootWidth);
        this.maxDepth = maxDepth;
    }
    
    public void Insert(Point p)
    {
        root.Insert(p);
    }
    
    public List<Point> Query(float minX, float maxX, float minY, float maxY)
    {
        return root.Query(minX, maxX, minY, maxY);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
class Point {
    constructor(
        public x: number,
        public y: number
    ) {}
}

class Quadtree {
    private root: Node;
    private maxDepth: number;

    constructor(rootX: number, rootY: number, rootWidth: number, maxDepth: number = 16) {
        this.root = new Node(rootX, rootY, rootWidth);
        this.maxDepth = maxDepth;
    }

    insert(point: Point): void {
        this.root.insert(point);
    }

    query(minX: number, maxX: number, minY: number, maxY: number): Point[] {
        return this.root.query(minX, maxX, minY, maxY);
    }
}

class Node {
    private points: Point[] = [];
    private ne: Node | null = null;
    private nw: Node | null = null;
    private se: Node | null = null;
    private sw: Node | null = null;
    private readonly maxCapacity = 4;

    constructor(
        public x: number,
        public y: number,
        public width: number
    ) {}

    insert(point: Point): boolean {
        if (!this.contains(point)) return false;

        if (this.points.length < this.maxCapacity && !this.ne) {
            this.points.push(point);
            return true;
        }

        if (!this.ne) {
            this.split();
        }

        if (this.ne!.insert(point)) return true;
        if (this.nw!.insert(point)) return true;
        if (this.se!.insert(point)) return true;
        if (this.sw!.insert(point)) return true;

        return false;
    }

    private contains(point: Point): boolean {
        return point.x >= this.x - this.width/2 && 
               point.x <= this.x + this.width/2 &&
               point.y >= this.y - this.width/2 &&
               point.y <= this.y + this.width/2;
    }

    private split(): void {
        const half = this.width / 2;

        this.ne = new Node(this.x + half/2, this.y + half/2, half);
        this.nw = new Node(this.x - half/2, this.y + half/2, half);
        this.se = new Node(this.x + half/2, this.y - half/2, half);
        this.sw = new Node(this.x - half/2, this.y - half/2, half);

        for (const point of this.points) {
            this.ne.insert(point);
            this.nw.insert(point);
            this.se.insert(point);
            this.sw.insert(point);
        }

        this.points = [];
    }

    query(minX: number, maxX: number, minY: number, maxY: number): Point[] {
        const result: Point[] = [];

        if (!this.intersects(minX, maxX, minY, maxY)) return result;

        if (!this.ne) {
            for (const point of this.points) {
                if (point.x >= minX && point.x <= maxX && 
                    point.y >= minY && point.y <= maxY) {
                    result.push(point);
                }
            }
            return result;
        }

        result.push(...this.ne.query(minX, maxX, minY, maxY));
        result.push(...this.nw.query(minX, maxX, minY, maxY));
        result.push(...this.se.query(minX, maxX, minY, maxY));
        result.push(...this.sw.query(minX, maxX, minY, maxY));

        return result;
    }

    private intersects(minX: number, maxX: number, minY: number, maxY: number): boolean {
        return !(maxX < this.x - this.width/2 || 
                minX > this.x + this.width/2 ||
                maxY < this.y - this.width/2 ||
                minY > this.y + this.width/2);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
Point = {}
Point.__index = Point

function Point.new(x, y)
    local self = setmetatable({}, Point)
    self.x = x
    self.y = y
    return self
end

Node = {}
Node.__index = Node

function Node.new(x, y, width)
    local self = setmetatable({}, Node)
    self.x = x
    self.y = y
    self.width = width
    self.points = {}
    self.ne = nil
    self.nw = nil
    self.se = nil
    self.sw = nil
    self.max_capacity = 4
    return self
end

function Node:insert(point)
    if not self:contains(point) then return false end

    if #self.points < self.max_capacity and not self.ne then
        table.insert(self.points, point)
        return true
    end

    if not self.ne then
        self:split()
    end

    if self.ne:insert(point) then return true end
    if self.nw:insert(point) then return true end
    if self.se:insert(point) then return true end
    if self.sw:insert(point) then return true end

    return false
end

function Node:contains(point)
    return point.x >= self.x - self.width/2 and 
           point.x <= self.x + self.width/2 and
           point.y >= self.y - self.width/2 and
           point.y <= self.y + self.width/2
end

function Node:split()
    local half = self.width / 2

    self.ne = Node.new(self.x + half/2, self.y + half/2, half)
    self.nw = Node.new(self.x - half/2, self.y + half/2, half)
    self.se = Node.new(self.x + half/2, self.y - half/2, half)
    self.sw = Node.new(self.x - half/2, self.y - half/2, half)

    for _, point in ipairs(self.points) do
        self.ne:insert(point)
        self.nw:insert(point)
        self.se:insert(point)
        self.sw:insert(point)
    end

    self.points = {}
end

function Node:query(minX, maxX, minY, maxY)
    local result = {}

    if not self:intersects(minX, maxX, minY, maxY) then return result end

    if not self.ne then
        for _, point in ipairs(self.points) do
            if point.x >= minX and point.x <= maxX and 
               point.y >= minY and point.y <= maxY then
                table.insert(result, point)
            end
        end
        return result
    end

    for _, point in ipairs(self.ne:query(minX, maxX, minY, maxY)) do
        table.insert(result, point)
    end
    for _, point in ipairs(self.nw:query(minX, maxX, minY, maxY)) do
        table.insert(result, point)
    end
    for _, point in ipairs(self.se:query(minX, maxX, minY, maxY)) do
        table.insert(result, point)
    end
    for _, point in ipairs(self.sw:query(minX, maxX, minY, maxY)) do
        table.insert(result, point)
    end

    return result
end

function Node:intersects(minX, maxX, minY, maxY)
    return not (maxX < self.x - self.width/2 or 
               minX > self.x + self.width/2 or
               maxY < self.y - self.width/2 or
               minY > self.y + self.width/2)
end

Quadtree = {}
Quadtree.__index = Quadtree

function Quadtree.new(rootX, rootY, rootWidth, maxDepth)
    maxDepth = maxDepth or 16
    local self = setmetatable({}, Quadtree)
    self.root = Node.new(rootX, rootY, rootWidth)
    self.maxDepth = maxDepth
    return self
end

function Quadtree:insert(point)
    self.root:insert(point)
end

function Quadtree:query(minX, maxX, minY, maxY)
    return self.root:query(minX, maxX, minY, maxY)
end
  • 标题: 【游戏算法】 - 四叉树
  • 作者: 宋
  • 创建于 : 2020-11-27 22:16:55
  • 更新于 : 2021-03-15 20:30:55
  • 链接: https://sxl-space.tk/2020/11/27/001_2D-QuadTree/
  • 版权声明: 版权所有 © 宋，禁止转载。
目录
【游戏算法】 - 四叉树
  1. 1. 四叉树
    1. 1.1. 代码实现